Наука | Диалоги о науке | Анизотропия и поляризация реликтового излучения

Анизотропия и поляризация реликтового излучения.

Последние данные

М.В. Сажин

Исследование анизотропии и поляризации реликтового излучения является одним из самых мощных инструментов современной космологии. В настоящее время проводится и готовится большое количе­ство экспериментов, цель которых — наблюдения анизотропии и поляризации реликтового излучения. Анализ анизотропии и поляризации реликтового излучения позволит получить значения фундаменталь­ных параметров современной и ранней Вселенной, в частности позволит пролить свет на важнейшую проблему современной физики — существование гравитационных волн. Результат исследования анизо­тропии и поляризации реликтового излучения может внести существенный вклад в физику элементарных частиц и в физику высоких энергий. В предлагаемой статье вкратце описаны механизмы образования анизотропии и поляризации. Особое внимание в статье уделяется последним экспериментам в области наблюдения анизотропии и поляризации реликтового излучения, в частности результатам эксперимента WMAP — наблюдения анизотропии и поляризации реликтового излучения с борта специализированного космического аппарата.

Содержание

1. Введение (197).

2. Открытие анизотропии и недавние эксперименты (198).

3. Эксперимент WMAP (200).

3.1. Описание эксперимента. 3.2. Результаты первого года рабо­ты.

4. Будущие эксперименты и определение параметров инфляции (203).

5. Заключение (204). Список литературы (205).

1. Введение

Мы живем в расширяющейся Вселенной. Ее кинетиче­ские и динамические свойства характеризуются масш­табным фактором a(t) и его зависимостью от времени. Отношение масштабного фактора в современный момент времени к масштабному фактору какой-либо из прошлых эпох называется красным смещением этой эпохи и обозначается z.

В прошлом, когда масштабный фактор был примерно в 1000 раз меньше, чем сейчас, в высокотемпера-

турной плазме Вселенной, состоящей из электронов, протонов, массивных слабовзаимодействующих частиц и фотонов, количество фотонов было гораздо больше, чем количество барионов (в несколько миллиардов раз), и именно поэтому Вселенная называется "горячей". При расширении температура падает и Вселенная остывает. Темп расширения значительно медленнее характерного времени установления равновесия в горячей плазме, поэтому частицы в ней находятся в термодинамическом равновесии. Одной из таких частиц является фотон. Именно эти фотоны и называются реликтовыми.

Несмотря на то что в вакууме фотон распростра­няется со скоростью света, в горячей плотной плазме из-за рассеяния на электронах фотоны рапространяются гораздо медленнее. Когда Вселенная расширяется на­столько, что плазма остывает до температуры рекомби­нации, электроны начинают соединяться с протонами, образуя нейтральный водород, а фотоны начинают распространяться свободно. Точки, из которых фотоны доходят до наблюдателя, образуют так называемую поверхность последнего рассеяния. Это единственный источник во Вселенной, окружающий нас со всех сторон.

В момент рекомбинации температура поверхности последнего рассеяния равна примерно 3000 К. Сейчас она в 1000 раз меньше. Это уменьшение произошло из-за расширения Вселенной.

Реликтовое излучение обладает уникальным свой­ством. Его температура удивительно изотропна. Она изотропна с точностью 10~3. Тем не менее небольшая анизотропия существует. Анизотропия — это разница температуры в разных направлениях на небе. Ее вели­чина равна примерно 3 мК. Это происходит из-за того,

что Земля, солнечная система, наша Галактика дви­гаются сквозь реликтовое излучение с некоторой пеку­лярной скоростью. 3 мК — это кинетическая составляю­щая анизотропии реликтового излучения, которая назы­вается дипольной анизотропией: впереди нас (по ходу движения) температура чуть-чуть выше, за нами (против хода движения) температура чуть-чуть ниже.

Помимо кинетической составляющей, есть и потен­циальные члены в анизотропии реликтового излучения, обязанные своим происхождением гравитационным полям очень больших масштабов, которые сравнимы с горизонтом частиц, другими словами, с расстоянием до поверхности последнего рассеяния. Если мы рассмотрим такое гравитационное поле, то низшая мультипольная гармоника для этого гравитационного поля будет ква-друпольной. Происходит так потому1, что дипольной гармоники в гравитационном поле нет. Она возникает только в тех полях, которые имеют заряды разных знаков. Гравитационное поле создается массами, имею­щими положительный знак. Степень неоднородности гравитационного поля характеризуется приливными силами, низшая гармоника в приливных силах — ква-друпольная.

Рассмотрим основное уравнение, описывающее анизотропию реликтового излучения, и основные физиче­ские эффекты, которые ее вызывают. Уравнение измене­ния температуры в направлении вектора е имеет вид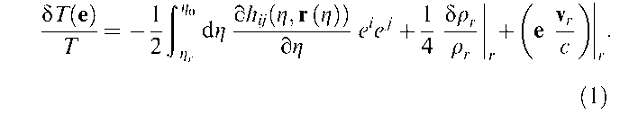

Первый член в этом уравнении описывает эффект Сакса-Вольфа2, который был предсказан еще в начале 60-х годов Саксом и Вольфом и заключающийся просто в том, что фотоны, двигаясь в переменном потенциале, либо приобретают, либо теряют энергию.

Второй член обусловлен эффектом Силка. Представь­те, что на поверхности последнего рассеяния уже есть некоторые флуктуации плотности. Там, где есть флук­туации плотности барионов, есть и флуктуации плотно­сти фотонов, поскольку считается (и это доказано), что энтропия по пространству удивительно однородна, гораздо в более высокой степени однородна, чем анизо­тропия реликтового излучения. Там, где будет больше барионов, будет больше и фотонов, — в этом и заклю­чается эффект Силка.

Третье слагаемое обязано своим происхождением эффекту Доплера. Поверхность последнего рассеяния, точнее, вещество, которое формирует ее, может двигать­ся. Если часть этой поверхности движется к нам, то фотоны, которые излучаются с нее, становятся более голубыми, если какая-либо часть движется от нас — более красными. В зависимости от скорости, точнее, от проекции вектора скорости на луч зрения, получается более голубое или более красное смещение, а для температуры это выглядит как анизотропия в данном направлении.

Поскольку поверхность последнего рассеяния есть сфера, то проще всего анализировать то, что мы наблю­даем, разложив в ряд по сферическим функциям, кото­рые являются полным и ортогональным набором функций на сфере: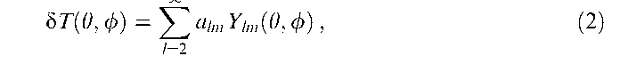

где aim — коэффициенты, называемые мультипольными коэффициентами, a Y\m — сферические гармоники. Надо также отметить, что удобнее представлять и сравнивать результаты наблюдений и теоретические расчеты в терминах величин, которые являются вращательно-инва-риантными и не зависят от частного выбора системы отсчета. Стоит напомнить, что в астрономии есть не­сколько систем: экваториальная, связанная с Землей, эклиптическая, связанная с положением плоскости орбиты Земли, галактическая, и в каждой из этих систем коэффициенты щт будут свои. Дело в том, что они не вращательно-инвариантны. Поэтому обычно выделяют так называемую вращательно-инвариантную величину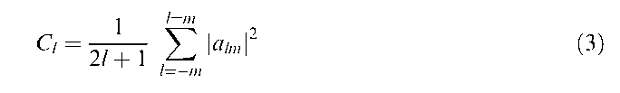

и работают именно с ней. Спектр строят для величины / (/ + 1)С//2я. Это связано с тем, что, если умножить С/ на /(/+1), то образуется так называемое плато Харри-сона-Зельдовича, которое на графике будет выглядеть горизонтальной линией. Именно в такой нормировке, как вы увидите, и представляется большинство экспери­ментальных данных по мультипольным спектрам.

Более подробно с современными взглядами на строе­ние и эволюцию Вселенной можно ознакомиться в книгах [1-5].

2. Открытие анизотропии и недавние эксперименты

Надо добавить, что само реликтовое излучение, обнару­женное в 1965 г., явилось самым важным открытием в космологии после открытия Хабблом расширения нашей Вселенной. Дипольная анизотропия реликтового излуче­ния (движение сквозь реликтовое излучение) была уста­новлена в 1972 г. (Современное значение амплитуды дипольной гармоники составляет ~ 3 мК.) После этого радиоастрономы 20 лет улучшали радиометры и зареги­стрировали анизотропию реликтового излучения, свя­занную с более высокими гармониками и с первичными флуктуациями гравитационных полей, которые содер­жат в себе информацию о ранней Вселенной.

Крупномасштабная анизотропия реликтового излу­чения была обнаружена в 1992 г. по результатам работы спутника "Реликт". В январе 1992 г. наша группа на семи­наре в ГАИШ объявила, что мы зарегистрировали анизотропию реликтового излучения, хотя отношение сигнала к шуму в нашем эксперименте было неболь­шое — порядка трех. Мы опубликовали статью в Письмах в астрономический журнал и параллельно послали ее в Monthly Notices, где она также была напечатана через несколько месяцев [6, 7].

К тому времени на орбите работал американский спутник СОВЕ (сокращение от английских слов COsmic Background Explorer). Это был аппарат, аналогичный спутнику "Реликт", только усовершенствованный. Он имел три частотных канала, в каждом из которых было два радиометра. Вскоре после нашей статьи [6] была опубликована статья группы СОВЕ [8] с изложением результатов работы спутника, в которой сообщалось о детектировании анизотропии реликтового излучения.

Многочастотность позволила группе СОВЕ уверенно отделить анизотропию на поверхности последнего рас­сеяния от анизотропии галактического и внегалактиче­ского радиоизлучения. Этот факт, а также большее отношение сигнал/шум после завершения эксперимента (СОВЕ работал на орбите свыше 4 лет) позволяет американским исследователям связывать открытие ани­зотропии реликтового излучения с результатами аппа­рата СОВЕ.

После 1992 г. проведено много экспериментов по наблюдению анизотропии реликтового излучения с поверхности Земли и баллонов, но чувствительность радиометров в этих экспериментах была примерно такая же, как у аппаратов "Реликт" и СОВЕ. Тем не менее был построен спектр мультипольных гармоник, совпадающий с теоретическим, который содержал плато Харрисона - Зельдовича, и открыт первый доплеровский пик (рис. 1). Однако данные этих экспериментов опреде­лены с большими ошибками из-за низкой чувствительно­сти радиометров.

Новое поколение радиометров реализовано в баллон­ном эксперименте BOOMERang [9]. В 1998 г. был осуществлен полет воздушного шара, который нес гондолу с аппаратурой эксперимента BOOMERang. Шар летал над Антарктидой, сделал полный оборот, и исследователи составили карту радиояркости неболь­шого участка небесной сферы. То, что удалось изме­рить, — маленький участок неба, который составляет лишь 5 % площади всей небесной сферы. Но тем не менее участок был выбран удачно, на нем отсутствовали сильные внегалактические источники радиоизлучения и интенсивность синхротронного излучения была также минимальной.

В результате был измерен спектр анизотропии релик­тового излучения (так называемая С/-спектроскопия), который показал наличие первого, второго и третьего доплеровских пиков. Сейчас экспериментаторы утверж­дают, что наблюдаются пять пиков. Поскольку размер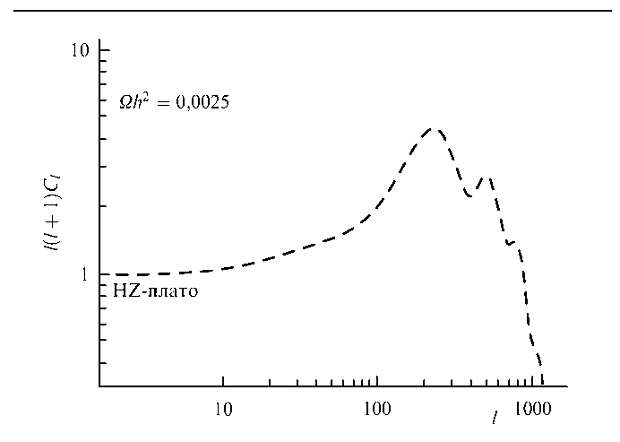

Рис. 1. Теоретический

спектр анизотропии реликтового излучения в соответствии с предсказанием

стандартной космологической моде­ли.

карты участка небесной сферы был мал, то и минималь­ное значение мультипольного числа, измеренное в экспе­рименте, /« 26. Поэтому сшивка с плато Харрисона-Зельдовича была приближенной.

Вскоре после этого был проведен баллонный экспе­римент Archeops [10, 11] (см. также web site эксперимента "Археопс" [12]). Он разрабатывался во Франции при участии многих европейских исследователей. Среди создателей этого эксперимента имеются также россий­ские космологи А.А. Старобинский и И.А. Струков. Этот эксперимент рассматривается как предшественник высо­кочастотной части эксперимента "Планк".

За время этого эксперимента осуществлено несколько полетов воздушного шара, последний — в феврале 2002 г. Шар был запущен в Швеции и подобран в Норильске.

Экспериментаторы быстро обработали свои данные. В ходе эксперимента была достигнута рекордная чувст­вительность порядка 100 мкК. В результате было сде­лано приблизительно 30 % карты неба с угловым разре­шением 8 минут дуги на частоте 143 ГГц.

Результаты обработки представлены на рис. 2: по вертикальной оси отложена величина / (/ + 1) С/, делен­ная на 2л. Измерения позволили определить амплитуды мультипольных коэффициентов от / = 10 до / ˆ 150. На рисунке видно часть плато Харрисона - Зельдовича — почти постоянное значение величины / (/ + 1) С/ с 1 — 2 до /« 30. Разность спектров, обработанных двумя различными методиками (показанная на нижнем гра­фике), сравнима с нулем.

По спектру Q определяются спектр флуктуации во Вселенной, а также глобальные космологические пара­метры: полная плотность Вселенной и ее составляющие, такие как плотность барионов, плотность темного веще­ства, плотность, соответствующая Л-члену, и т.п. Так, по положению первого доплеровского пика достаточно точно находится полная плотность Вселенной, а по его амплитуде — содержание барионов.

Прежде чем перейти к эксперименту MAP, необхо­димо рассказать еще об одном эксперименте, который называется DASI [13, 14]. Дело в том, что в этом эксперименте была зарегистрирована поляризация реликтового излучения. Сама анизотропия реликтового излучения очень маленькая, амплитуда первого допле-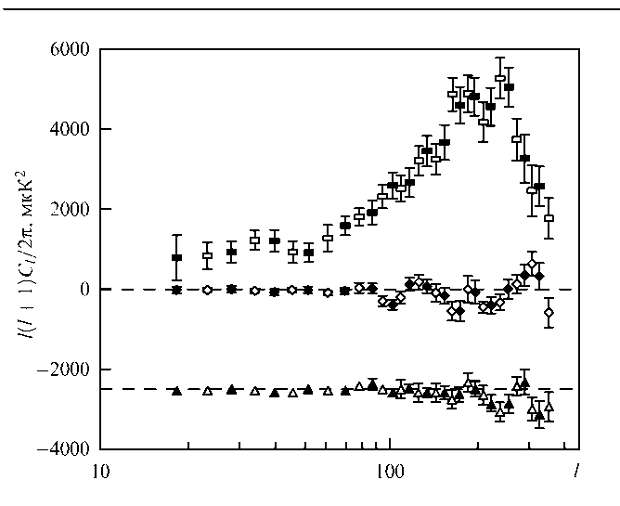

Рис. 2. Спектр

мультипольных гармоник, полученный в ходе экспе­римента "Археопс".

ровского пика порядка 75 мкК, амплитуда плато Харри-сона-Зельдовича — порядка 20 мкК. Другими словами, относительная анизотропия составляет ~ 10~5. Поляри­зация реликтового излучения, дающая очень ценную информацию о современной и ранней Вселенной, имеет еще меньшую амплитуду.

В эксперименте DASI, в котором впервые была зарегистрирована поляризация реликтового излучения, проводилась Q-спектроскопия с мультипольной гармо­ники / = 150 до / = 1000 на различных частотах.

Следует напомнить, что электромагнитное излучение характеризуется не только интенсивностью, но и еще тремя параметрами, которые называются параметрами Стокса: 2, ?/и V. К отвечает за круговую поляризацию, Q и U описывают линейную поляризацию. Сразу огово­римся, что у реликтового излучения образуется только линейная поляризация во время эпохи просветления, когда оптическая толща по томсоновскому рассеянию меняется примерно с 3 до 0,1, поэтому космологи полагают, что V = 0. Величины Q, U и V являются тензорами второго ранга на сфере. Интенсивность реликтового излучения можно разложить по сфериче­ским скалярным гармоникам, а величины Q и U следует разложить по так называемым спиновым гармоникам второго ранга, что отвечает вращательно-инвариантным разложениям тензора второго ранга [15-17]: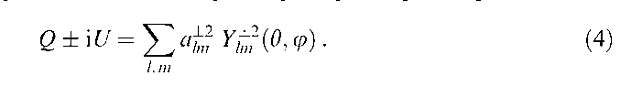

Помимо того, что здесь

вводятся новые функции, по которым идет разложение, в поляризации

выделяются еще так называемые Е- и В-моды [17]:

Помимо того, что здесь вводятся новые функции, по которым идет разложение, в поляризации выделяются еще так называемые Е- и В-моды [17]:

Эти моды соответствуют двум принципиально разным по симметрии величинам. Мода В является антисиммет­ричной относительно преобразований четности. Это очень важно, поскольку различие между модами Е и В позволит в дальнейшем различить вклад возмущений плотности в анизотропию и поляризацию реликтового излучения от вклада гравитационных волн. Дело в том, что возмущения плотности генерируют только Е-моду поляризации реликтового излучения, тогда как гравита­ционные волны генерируют как Е-, так и ?-моду. Поэтому измерение поляризации позволяет определить спектр возмущений плотности отдельно от спектра гравитационных волн.

DASI — это наземный эксперимент, который прово­дился на Южном полюсе. В эксперименте была зареги­стрирована ?-мода поляризации. ?-мода не обнаружена. Для того чтобы убедиться, что наблюдается поляризация излучения с поверхности последнего рассеяния, а не син-хротронного, исследователи строят так называемый час­тотный индекс яркостной температуры ˆ-моды и смот­рят, совместим ли он с нулем. Для реликтового излучения частотный индекс точно равен нулю, потому что темпе­ратура реликтового излучения — температура черно-тельного излучения — не зависит от частоты, а эффектив­ная температура любого другого излучения, такого, например, как синхротронное, зависит от частоты.

3. Эксперимент WMAP 3.1. Описание эксперимента

Название спутника WMAP — это аббревиатура от Wilkinson Microwave Anisotropy Probe [18]. Первона­чально спутник назывался MAP. Знаменитый американ­ский ученый Дэвид Вилкинсон, который был одним из авторов проекта MAP, умер в сентябре 2002 года и в память о нем его ученики и соавторы решили назвать спутник его именем.

Спутник представляет собой аппарат массой 830 кг (рис. 3). Он был запущен в 2001 г. и выведен в точку L2, которая находится на расстоянии 1,5 млн км от Земли в стороне, противоположной Солнцу.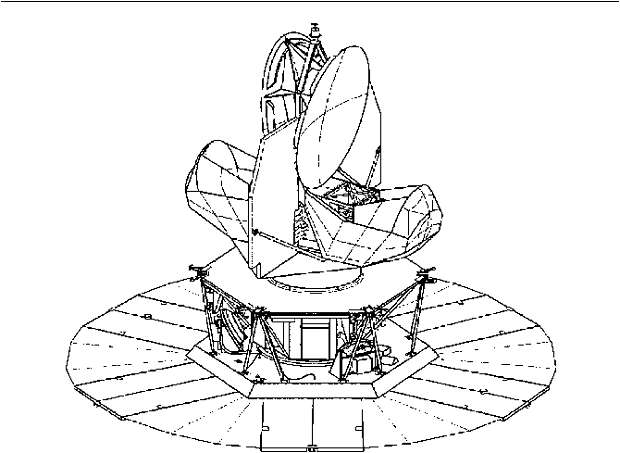

Рис. 3. Спутник WMAP

Время жизни спутника в рабочей точке предполага­лось не менее 2 лет, три дополнительных месяца отводи­лось для вывода спутника в расчетную точку.

Спутник предназначен для измерения анизотропии реликтового излучения и поляризации. Основная за­дача, которая была поставлена перед экспериментом, — составить карту всего неба с чувствительностью не хуже, чем 20 мкК, в каждом пикселе 3 и с систематическими ошибками, не превышающими 5 мкК в каждом пикселе. Принимающая система спутника состоит из двойного телескопа 1,4 х 1,6 м, сделанного по системе Грегори, в фокусе телескопа находится несколько радиометров на различные частоты. В таблице 1 приведены характери­стики радиометров.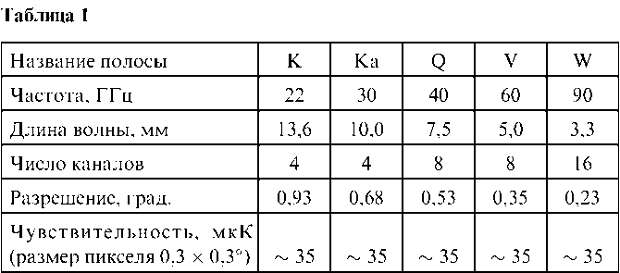

Рис. 4. Карты

небесной сферы, полученные на различных частотах в результате

проведения наблюдений на спутнике WMAP (располо­жены на периферии). В

центре находится синтетическая карта небес­ной сферы, сформированная из

карт на отдельных частотах.

Все частоты носят собственные имена. Две самых низких частоты К и Ка служили для мониторинга галактического излучения, а три высоких частоты Q, V, W — для построения карт излучения поверхности последнего рассеяния (рис. 4).

В феврале 2003 г. группа WMAP опубликовала пер­вые результаты эксперимента, причем сразу в нескольких статьях. Кроме этого много информации было поме­щено на web-страничке группы WMAP [18], откуда и взяты рисунки спутника WMAP, карты 57" и графики спектров анизотропии и кросс-корреляции анизотропии и поляризации.

3.2. Результаты первого года работы

Обсудим результаты, наиболее важные с точки зрения космологии. В статье [19] рассмотрено определение спектра мультипольных гармоник. Для построения карт на любой из частот использовались восемь дифферен­циальных агрегатов радиометров. Каждый агрегат состоял из двух радиометров, чувствительных к взаимно перпендикулярным модам линейной поляриза­ции.

После коррекции всех высокочастотных карт за распределенное галактическое излучение и вычитания точечных источников были восстановлены 28 кросс-корреляционных мультипольных спектров. Эти данные были объединены в единый спектр мультипольных гармоник (рис. 5). Необходимо обратить внимание на двугорбую структуру первого пика. Это явление, обна­руженное в эксперименте "Археопс", подтверждено и в эксперименте WMAP.

В статье [20] исследователи обсуждают детектирова­ние кросс-корреляции между анизотропией и ?-модой поляризации, так называемую кросс-корреляцию ТЕ. Значимость этой кросс-корреляции превышает 10 <т. Авторы подчеркивают, что обнаруженная зависимость хорошо совпадает с теоретическими предсказаниями в области средних углов (в < 5°), но значимо разнится в области больших углов (в > 10°). В области больших углов зафиксировано значительное увеличение кросс-корреляции. Для объяснения этого избытка космологи полагают наличие ионизованной среды в промежутке между нами и эпохой z ˆ 20. Оптическая толща по томсоновскому рассеянию составляет т«0,17. По­скольку оптическая толща вплоть до квазаров z« 6

Рис. 5. Спектр

мощности анизотропии: ¦ — данные WMAP, О —

данные CBI,

значительно меньше этой величины, то, по всей видимо­сти, степень ионизация во Вселенной эволюционировала достаточно сложным образом.

На рисунке 6 представлена измеренная кросс-корре­ляция. Сильный избыток в области больших углов (малых значений мультипольного числа /) явно указы­вает на наличие ионизованной плазмы между нами и поверхностью последнего рассеяния.

В статье [20] рассмотрены две простейших модели вторичной ионизации. Первая предполагает мгновенную полную ионизацию плазмы (хе = 1). Тогда красное смещение начала ионизации в этой модели приходится на z ~ 17. Но такая модель конфликтует с оптическими наблюдениями квазаров и измерениями оптической толщи в их направлениях. Поэтому авторы обсуждают другую модель, согласно которой ионизация эволюцио­нировала более сложным способом, что приводит к началу ионизации в момент z ˆ 20. Для создания такого сценария реионизации требуется новое поколение звезд, которые должны были образоваться при значениях красного смещения z « 30.

Наконец, в статье [21] обсуждаются значения гло­бальных космологических параметров, выведенных на основе результатов наблюдений спутника WMAP. Вна­чале рассматривается простая шестипараметрическая ACDM-модель, которая может объяснить наблюдае-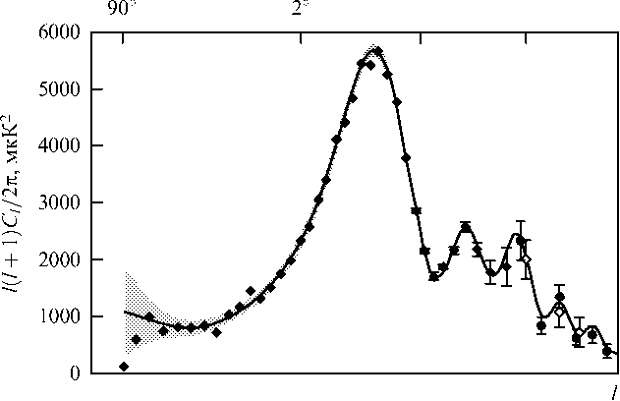

Рис. 6. Кросс-корреляция между анизотропией и Е-модой поляризации.

мую анизотропию (7Т-спектр) и кросс-корреляцию анизотропии и ˆ-моды поляризации (7ˆ-спектр). Эти параметры включают в себя плотность барионов Qˆh2, плотность холодной темной материи (CDM) Qmh2, параметр Хаббла h в единицах 100 км с-1 Мпк-1, ампли­туду спектра флуктуации плотности А, оптическую толщу по томсоновскому рассеянию во время вторич­ной ионизации вещества т и, наконец, спектральный индекс флуктуации плотности ns. Авторы утверждают, что большинство параметров хорошо определяются в рамках принятой модели. Исключение составляют два параметра: спектральный индекс ns и оптическая толща т. По этим параметрам существует явное вырождение. Так, функция правдоподобия меняется только на 0,05 при изменении оптической толщи в интервале 0,11 <т< 0,19. Авторы также специально оговари­ваются, что при определении параметра Хаббла они использовали измерения, полученные на телескопе Хаббла [22].

Поскольку анализ карт показал, что флуктуации на них являются гауссовыми, то авторы использовали это свойство для исследования поверхности наибольшего правдоподобия методом марковских цепей. Для каждой из моделей они строили TV-мерное распределение функ­ции правдоподобия в пространстве параметров. Наилуч­шая величина каждого параметра определялась как среднее значение:

Авторы утверждают, что простая модель дает при­емлемое описание экспериментальных данных ТТ- и TTi-спектров. Однако величины х2 для простой модели недопустимо велики. Так, для аппроксимации 7Т-спек-тра этой моделью нормированное на количество степе­ней свободы х2 — 1,09, что говорит о том, что вероят­ность принятия этой модели составляет только 3 %. Для аппроксимации ТТ- и TTi-спектров нормированное на количество степеней свободы х2 — 1,066, что несколько лучше. Тем не менее вероятность принятия этой модели для описания ТТ- и 7ˆ-спектров составляет только 5 %. Критерий у2 вычислялся по формуле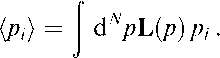

где v — число степеней свободы. Для модельных карт получено

-21п-=1.

V

Согласно утверждениям авторов это происходит из-за того, что простая шестипараметрическая модель не может описать резкие края, которые есть у наблюдае­мого спектра при значениях /« 120, вблизи максимума первого пика и при / « 350. Кроме того, авторы считают, что избыток в х2 обусловлен недооценкой шума на картах. Избыточный шум на картах, как они полагают, может быть связан с влиянием эффекта гравитационного линзирования на анизотропию реликтового излучения (с гравитационным линзированием можно ознакомиться в [23]), угловыми вариациями диаграммы направленности эксперимента WMAP, а также небольшого вклада негауссова шума на картах, возникающего при создании двумерных карт из одномерных сканов небесной сферы.

Таблица 2

Теперь приведем табл. 2 глобальных космологиче­ских параметров, полученных в рамках простой пара­метрической модели при обработке эксперимента WMAP.

Следует отметить, что космологи аппроксимировали экспериментальные данные в рамках плоского трехмер­ного пространства, другими словами, в рамках стандарт­ной космологической ACDM-модели.

Помимо этих первичных параметров, полученных из сравнения экспериментальных данных с теоретической моделью, исследователи приводят также список из 16 космологических параметров (табл. 3), которые выве­дены на основе первичных параметров, причем большин­ство выведено с помощью программы CMBFAST [17, 24], а также интегрирования уравнений Фридмана.

К этим параметрам следует добавить параметр плотности, ассоциируемый с A: Q\ = 0,663.

Таблица 3

Кроме простейшей модели с шестью параметрами авторы [21] рассмотрели и более сложные модели, которые содержали дополнительное число параметров, в частности модель с так называемым меняющимся спектральным индексом. Предполагалось, что зависи­мость флуктуации плотности от волнового вектора сложнее, чем степенной закон. Эту зависимость можно аппроксимировать почти степенным законом с неболь­шой девиацией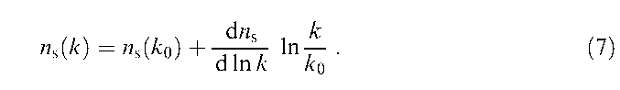

Мощность спектра скалярных возмущений фиксируется при значении волнового вектора ко = 0,05 Мпк-1.

Для определения малой добавки к спектральному индексу из наблюдений только данных WMAP недоста­точно. Необходимо привлекать другие результаты, в частности наземных экспериментов по наблюдению анизотропии реликтового излучения ACBAR и CBI, каталог распределения галактик 2dFGRS, а также дан­ные по распределению линий La в спектрах далеких квазаров.

Если использовать только данные экспериментов по анизотропии, то величина dns/d\nk будет составлять —0,031 (ˆ0025)' а ПРИ привлечении данных также и по ли­ниям La получается значение — 0,031 (ˆооп)* ˆак следует из приведенных данных, эффект, если он вообще сущест­вует, обнаружен на уровне достоверности ~ 2а. Конечно, привлечение данных экспериментов, выполненных по другой методике, несколько снижает ценность получен­ных результатов относительно переменного спектраль­ного индекса.

Авторы рассмотрели также возможный вклад грави­тационных волн космологического происхождения в анизотропию. Гравитационные волны должны рож­даться во время стадии инфляции [25, 26] за счет эффекта параметрического усиления гравитационных волн [27].

Гравитационно-волновой спектр в исследуемой модели имеет степенную зависимость от волнового вектора, а спектральный индекс4 связан с отношением амплитуд двух спектров как пt — —г/8, где г — отношение мощностей двух спектров при к — 0,002 Мпк-1. Вклад гравитационных волн в анизотропию не обнаружен, определен лишь верхний предел возможного вклада космологических гравитационных волн. Если рассмат­ривать только экспериментальные данные, то верхний предел есть г < 0,71; если накладывать дополнительные ограничения (например, считать, что скалярный спек­тральный индекс меньше единицы), то верхний предел на мощность гравитационных волн во Вселенной полу­чается еще более жестким: г < 0,33.

Более сложные модели нашей Вселенной характери­зуются большим набором глобальных космологических параметров. Увеличивая размерность пространства параметров, исследователи, естественно, повышают точ­ность аппроксимации экспериментальных данных. В то же время они встречаются с многочисленными "вырож­дениями" в пространстве параметров. Вырождение можно продемонстрировать на следующем примере.

Имеющийся в распоряжении космологов набор экспери­ментальных данных может удовлетворять двум доста­точно сильно различающимся моделям. Так, скажем, модель с квинтэссенцией с уравнением состояния w — —0,5 и набором других параметров Qm — 0,47, h = 0,57 удовлетворяет экспериментальным данным, полученным WMAP, так же хорошо, как и стандартная ACDM-модель. Естественно, что модель квинтэссенции с уравнением состояния w = —0,5 была отвергнута на том основании, что получающееся значение параметра Хаббла на 2а меньше, чем значение того же параметра, полученное на телескопе Хаббла [22]. По тем же сооб­ражениям была отвергнута, например, модель с непло­ским трехмерным пространством с набором параметров QA = 0, Gtotai = 1,28, Н0 = 32,5 км с"1 Мпк"1.

Используя данные WMAP и каталога галактик 2dFGRS, можно существенно ограничить вклад всех нейтрино в общую плотность Вселенной. В эпоху до­минантности вещества, т.е. после z = 3454, нейтрино должны образовывать крупномасштабную структуру из-за гравитационной неустойчивости. Одновременно их движение подавляет флуктуации вещества на мелких масштабах. Поэтому сравнивая флуктуации в масшта­бах, которые изучают в экспериментах по анизотропии, и в масштабах, которые изучают по скучиванию галактик, можно определить верхний предел на общую плотность нейтрино. Этот предел равен Qvh2 < 0,0076. Отметим, что указанная величина значительно превосходит вклад в общую плотность безмассовых нейтрино. Если нейтрино безмассовые, то их доля в параметре плотности соста­вляет Qvh2 < 0,00006.

В статье [21] было отмечено интересное явление. Стандартная ACDM-модель хорошо описывает экспери­ментальные данные на всем промежутке, но дает несов­падение на больших масштабах (в ~ 60°) и на малых угловых масштабах. Если несовпадение на малых масш­табах можно убрать, включив в рассмотрение нестепен­ной спектр возмущений, то несовпадение на больших масштабах представляется более загадочным. Авторы обсуждают несколько объяснений в рамках современной физики и приходят к выводу, что это, возможно, указание на эффекты новой физики.

4. Будущие эксперименты

и определение параметров инфляции

В результате проведения баллонных, наземных и спутни­кового экспериментов измерена анизотропия реликто­вого излучения и надежно обнаружена его поляризация. Правда, зарегистрирована только ?-мода поляризации. ?-мода поляризации не зарегистрирована. Готовятся новые эксперименты, часть из которых предназначена для детектирования обеих мод поляризации, другие — для более детального изучения анизотропии. До сих пор при обсуждении экспериментов мы касались только изучения Вселенной в период рекомбинации и в период после рекомбинации. Однако первичные возмущения плотности и гравитационные волны генерируются во время инфляции. Значит, они должны нести информа­цию об условиях, при которых происходит инфляция. Обсудим теперь, какие параметры Вселенной на инфля­ционной стадии мы можем извлечь из изучения анизо­тропии и рекомбинации реликтового излучения.

С теорией инфляции читатель может познакомиться по книгам [2, 3], опубликованным на русском языке, или

по оригинальным статьям, включенным в сборник избранных статей по теории инфляции [28].

Рассмотрим простейший случай, когда инфляция во Вселенной создается одним скалярным полем ф:

Здесь точкой обозначена производная по времени, а штрихом — частная производная потенциала У(ф) по полевой переменной ф,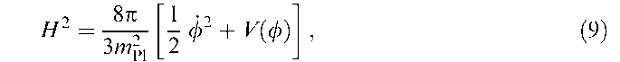

где mpi = 1,2 х 1019 ГэВ — масса Планка.

В большинстве моделей инфляции выполняются условия медленного изменения поля (в английском языке даже существует специальный термин "slow-roll approximation", иногда на русском языке это условие также называется режимом медленного скатывания). Эти условия можно записать как [29]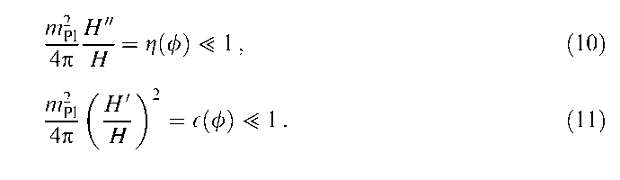

Если выполняется режим медленного изменения поля (10), (11), можно найти фурье-амплитуды возмущений плотности: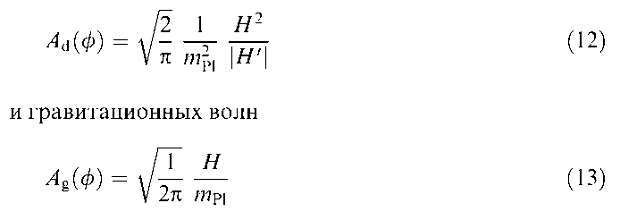

[25, 26, 29-31]. Можно связать длину волны возмущения X со скалярным полем ф согласно уравнению

Для случая режима медленного скатывания спектры возмущений плотности и гравитационных волн полу­чаются близкими к степенным. Спектр возмущений плотности принято записывать в виде А\ — A2kHs~l, а спектр гравитационных волн в виде А2 — В2кПт'. В случае предельно медленного скатывания получается спектр Харрисона - Зельдовича (HZ-спектр), который имеет соответственно спектральные показатели ns = 1 и пт 1. Космологи вводят также параметр

здесь к — волновой вектор соответствующего возмуще­ния, а Но — современное значение параметра Хаббла.

По анизотропии и поляризации реликтового излуче­ния астрономы могут восстановить спектры возмущений плотности и гравитационных волн. Отметим, что для однозначного восстановления необходимо знать как анизотропию, так и поляризацию [32].

Для раздельного измерения возмущений плотности и гравитационных волн особенно полезно измерение Е- и В-мод, поляризации. Напомним, что возмущения плот­ности дают вклад только в .Ё-моду, тогда как гравита­ционные волны генерируют как Е-, так и В-моду.

По спектрам возмущений плотности и гравитацион­ных волн можно восстановить значение потенциала скалярного поля, которое управляет инфляцией и его первой производной на достаточно большом интервале значений ф [33]. Сейчас, поскольку обнаружена только анизотропия и с некоторой достоверностью зарегистри­рована ?-мода поляризации, можно найти наклон потен­циала, который управляет инфляцией, но, к сожалению, нельзя определить его абсолютное значение. Возможно, это удастся сделать в будущем, когда начнут работать новые эксперименты, посвященные анизотропии и поля­ризации реликтового излучения, такие как PLANCK [34] и SPOrt [35].

Помимо восстановления потенциала инфляции SPOrt будет способен решить проблему излишней мощ­ности в поляризации на низких значениях мультиполь-ного числа, поскольку этот эксперимент предназначен специально для исследования поляризации в области малых значений мультипольного числа.

Спутник PLANCK составит карту всего неба на нескольких частотах с рекордным разрешением, состав­ляющим несколько угловых минут, и с высокой чувстви­тельностью. Это, возможно, позволит решить загадку двойной вершины первого доплеровского пика, понять несоответствие стандартной модели ACDM наблюде­ниям анизотропии и поляризации реликтового излуче­ния.

5. Заключение

В космологии произошли большие перемены. 20 - 30 лет назад одним из основных вопросов космологии был вопрос об определении топологии Вселенной: является ли наша Вселенная открытой или замкнутой? объем нашей Вселенной бесконечен или конечен? Решение этой проблемы заключалось в измерении параметра плотно­сти Q. Допустимые пределы в измерении этого параметра менялись 0,003 < Q < 10. Теперь полная плот­ность Вселенной известна с точностью до нескольких процентов: Q =1,02 ±0,02. Большинство остальных глобальных параметров Вселенной измеряются со срав­нимой точностью. В результате наблюдения анизотро­пии, в частности наблюдения анизотропии и поляриза­ции в эксперименте WMAP, открылась новая эпоха "прецизионной космологии". Теперь космология стано­вится точной наукой, неопределенность измерения основных параметров в космологии приближается к неопределенности измерения в физике. Это позволяет на количественном уровне изучать новые явления во Вселенной. Одним из приоритетов таких исследований является исследование квинтэссенции — нового вида материи, который пока невозможно изучать в земных лабораториях.

Новые космические и наземные эксперименты в изучении анизотропии и поляризации реликтового излучения позволят узнать о процессах в ранней Вселен­ной, а также лучше понять физические процессы, играющие основную роль на сверхбольших масштабах в нашей Вселенной.

Список литературы

1. Зельдович Я Б, Новиков И Д Строение и эволюция Вселенной (М.: Наука, 1975)

2. Долгов А Д, Зельдович Я Б, Сажин М В Космология ранней Вселенной (М.: Изд-во МГУ, 1988)

3. Линде А Д Космология и элементарные частицы (М.: Наука, 1985)

4. Вейнберг С Гравитация и космология (М.: Мир, 1975)

5. Сажин М В Современная космология в популярном изложении (М.: Едиториал УРСС, 2002)

6. Струков И А и др. Письма в Астрон. журн. 18 387 (1992)

7. Strukov I A et al. Моп. Not. R. Astron. Soc. 258 37P (1992)

8. Smoot G F et al. Astrophys. J. 396 LI (1992)

9. de Bernardis P et al. Nature 404 955 (2000)

10. Benoit A et al. Astron. Astrophys. 399 L19 (2003); astro-ph/0210305

11. Benoit A et al. Astron. Astrophys. 399 L25 (2003); astro-ph/0210306

12. http://archeops03.free.fr/main_archeops/index_english.html

13. Leitch E M et al. Nature 420 763 (2002); astro-ph/0209476

14. Kovac J et al. Nature 420 772 (2002); astro-ph/0209478

15. Сажин M В, Шульга В В Вестник МГУ. Сер. 3. Физ. Астрон. 37

(3) 69 (1996)

16. Сажин М В, Шульга В В Вестник МГУ. Сер. 3. Физ. Астрон. 37

(4) 87 (1996)

17. Seljak U, Zaldarriaga М Phys. Rev. Lett. 78 2054 (1997)

18. Wilkinson Microwave Anisotropy Probe, http://map.gsfc.nasa.gov and references therein

19. Hinshaw G et al., First Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: The Angular Power Spectrum, astro-ph/0302??

20. Kogut A et al, First Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: ТЕ Polarization

21. Spergel D N et al., First Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters

22. Freedman W L et al. Astrophys. J. 553 47 (2001)

23. Захаров А Ф, Сажин M В У ФИ 168 1041 (1998)

24. Seljak U, Zaldarriaga M, http://physics.nyu.edu/matiasz/ CMBFAST/cmbfast.html

25. Старобинский А А Письма в ЖЭТФ 30 719 (1979)

26. Rubakov V A, Sazhin M V, Veryaskin A V Phys. Lett. В 115 189 (1982)

27. Грищук Л П ЖЭТФ 67 825 (1974)

28. Abbott L F, Pi S-Y Inflationary Cosmology (Singapore: World Scientific, 1986)

29. Copeland E J et al. Phys. Rev. D 48 2529 (1993)

30. Dodelson S, Knox L, Kolb E W Phys. Rev. Lett. 72 3444 (1994)

31. Starobinsky A A Phys. Lett. В 111 175 (1982)

32. Sazhin M V, Benitez N Astrophys. Lett. Commun. 32 105 (1995)

33. Melchiorri A et al. Astrophys. J. 518 562 (1999)

34. http://astro.estec.esa.nl/SA-general/Projects/Planck/

35. SKY Polarization Observatory, http://sport.bo.iasf.cnr.it/